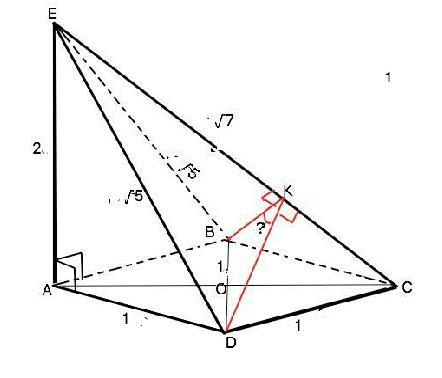
Вариант решения.
Угол между плоскостями EBC и ECD - двугранный. Его величина равна величине линейного угла между ними, т.е. равна величине угла, сторонами которого являются лучи с общим началом на ребре двугранного угла, проведенные в его гранях перпендикулярно ребру.
Т.к. острый угол ромба 60°, диагональ ВD делит ромб на два равносторонних треугольника. Примем стороны ромба равными 1. Тогда АЕ=2, ВD=АВ=1, AC=2AO=2•sin60°=√3.
Треугольники АЕВ и АЕD равны по равным катетам.
По т.Пифагора ЕD=ЕВ=√(AE²+AD²)=√(4+1)=√5
EC=√(AE²+AC²)=√(4+3)=√7
Треугольники ЕСD и ЕСВ равны по трем сторонам. Поэтому основания их высот, проведенные из равных углов ( ∠СBЕ=∠СDЕ) к общей стороне ЕС, совпадут. Отрезки КВ и КD перпендикулярны ребру ЕС двугранного угла в одной точке К. Угол ВKD - искомый.
1) По т.косинусов ЕD²=EC²+CD² -2ED•CD•cosECD. ⇒
5=7+1- 2•1•√7•cosECD ⇒ cosECD= (5-8): (-2√7)=3/2√7
Из прямоугольного ∆ СКD длина DK=ВК=СD•sinECD. Из формулы sin²x+cos²x=1 находим sinECD=√(1-9/28)=(√19)/2√7.⇒ DK=BK=1•(√19)/2√7. Из ∆ ВКD BD²=BK²+DK²- 2BK•DK•cosBKD ⇒ 1=19/28+19/28-2•19/28•cosBKD, ⇒ 1=2•19/28•(1-cosBKD) откуда cos∠BKD=1-14/19=5/19 ∠BKD=arccos 5/19