Высота проведенная из вершины на основание равнобедренного треугольника равна 16см, а...

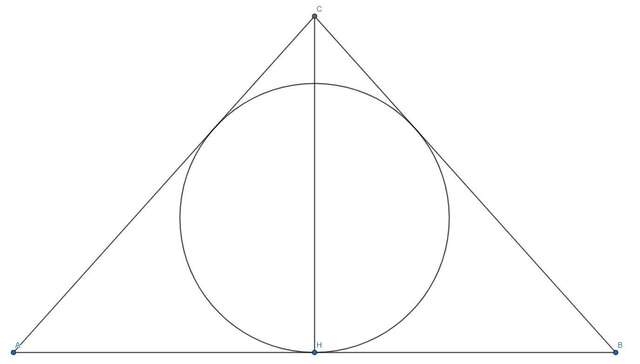
Пусть основание равно 4x, тогда боковая сторона равна 3x.

Площадь треугольника равна $\frac{1}{2}ah$ , где a - основание, h - высота.

$S_{ABC}=\frac{1}{2}*4x *16=32x$

В то же время $S=\frac{1}{2}Pr$ , где P - периметр треугольника, r - радиус вписанной окружность.

Периметр треугольника равен сумме всех его сторон: 4x+3x+3x=10x, т.к боковые стороны треугольника равны.

Таким образом,

$S_{ABC}=\frac{1}{2}*10x*r=5x*r$

Составим уравнение:

$5xr=32x\\r= \frac{32}{5}=6.4$

Ответ: 6,4 см

Высота проведенная из вершины ** основание равнобедренного треугольника равна 16см, а...