y`=(x³/3ˣ)`=(3x²·3ˣ-x³·3ˣ·ln3)/(3ˣ)²
y`=0
3x²·3ˣ-x³·3ˣlnx=0
3ˣ·x²(3-x·ln3)=0
3ˣ>0 при любом х
х=0 или 3-x·ln3=0
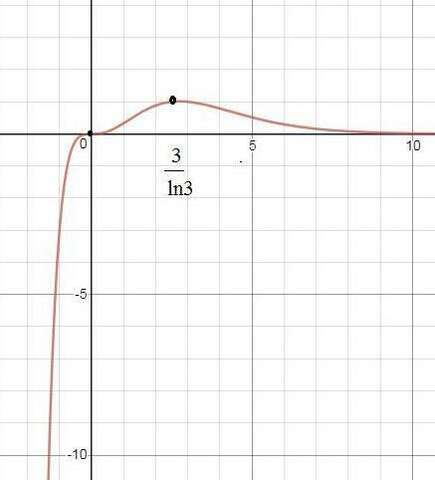
х=0 или х=3/ln3
При переходе через точку х=3/ln3
производная меняет знак с + на - ,
значит в точке х=3/ln3 функция имеет максимум.
См. рис.
x=0 - точка перегиба, так как вторая производная меняет знак
y``=(6x·3ˣ+3x²·3ˣ·ln3-3x²·3ˣ·ln3-x³·3ˣ·ln²3)/(3ˣ)⁴
y=0 - горизонтальная асимптота, других асимптот нет.