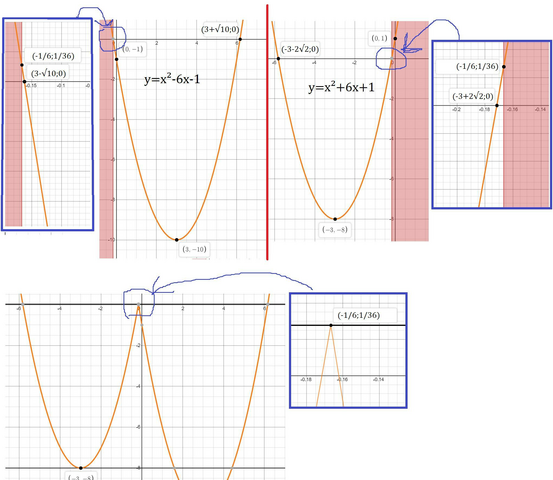
Функция из верхней системы, это парабола, ветви которой направлены вверх, координата вершины (3;-10), пересекает оси координат в точках (3-√10;0),(0;-1),(3+√10;0). Найдём ординату границы области определения этой функции из нашей системы:
Теперь рассмотри функцию из второй системы, это парабола, ветви которой направлены вверх, координат вершины (-3;-8), пересекает оси координат в точках (-3-2√2;0),(-3+2√2;0),(0;1)
Абсциссу границ можем не считать, дело в том, что в этой точке модуль раскрывается как ноль, поэтому не важно раскрыли мы его с плюсом или с минусом значение будет все равно 0, а значит значение функции будет одинаковым.
Теперь надо сравнить нули функции с абсциссой границы, чтобы узнать какие нули войдут в ограничение.
2\\\Rightarrow \frac{-1}{6}>(-3+2\sqrt{2})" alt="\frac{-1}{6}V(3-\sqrt{10});\sqrt{10}V\frac{19}{6};10<\frac{361}{36}\\\Rightarrow \frac{-1}{6}<(3-\sqrt{10})\\\\\frac{-1}{6}V(-3+2\sqrt{2});\frac{17}{12}V\sqrt{2};\frac{289}{144}>2\\\Rightarrow \frac{-1}{6}>(-3+2\sqrt{2})" align="absmiddle" class="latex-formula">
Из сравнения кстати следует, что все нули левой параболы левее всех нулей правой параболы
Смотри графики внизу.
Параболы строили по трём точкам (вершина и нули).
Прямая y=m параллельна или совпадает с ось Ох, посмотрев на график можно определить, что при m= -8 и m=1/36, будет всего три общие точки.
