Ответ:
Пошаговое объяснение:
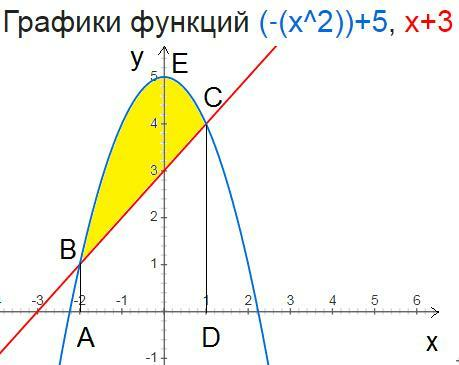
найдем точки пересечения графиков
приравняем правые части формул
-х²+5=х+3
х²+х-2=0; d=1+4*2=9; x₁,₂=(-1±√9)/2=(-1±3)/2; x₁=-2; x₂=1
Площадь криволинейной трапеции ABECD по формуле Ньютона-Лейбница
1 1
SABECD=∫(-x^2+5)dx=(-(x³/3)+5x)) =-1/3+5-(-(-2)³/3+5(-2))=-1/3+5-8/3+10=
-2 -2
=15-9/3=15-3=12
рассмотрим трапецию ABCD
точки B,C ∈ прямой y=x+3 ⇒
AB=y(-2)=-2+3=1 ; СD=y(1)=1+3=4; AD=x₂-x₁ =1-(-2)=3
площадь трапеции ABCD
SABCD=(a+b)h/2=(AB+CD)AD/2=(1+4)3/2=5*3/2=7,5
площадь фигуры ограниченной линиями y=-х²+5 и y=х+3
SBEC=SABECD-SABCD=12-7,5=4.5 кв. ед.