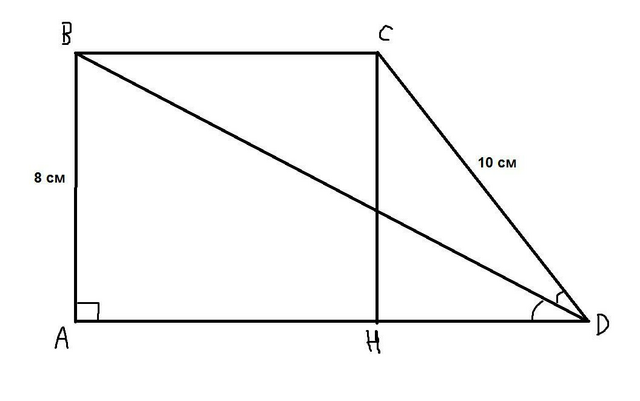
3. Решение:
Пусть трапеция будет трапецией ABCD, и СН - её высота, тогда
BD - биссектриса острого угла трапеции.
Так как AD║BC, то ∠BDA = ∠DBC (как накрест лежащие)
Отсюда ΔBCD - равнобедренный и ВС=DC=10 см
ABCH - прямоугольник, значит АН=ВС=10 см и АВ=СН=8 см
По теореме Пифагора HD² = CD² - CH² = 100 см² - 64 см²=36 см²
HD=6 см
AD=AH + HD=10 см + 6 см=16 см
Значит S ABCD= 1/2 × (AD + BC) × CH= 1/2 × (16 см + 10 см) × 8 см=104 см²
Ответ: 104 см²