Дан многочлен P(X)=2x квадрат -4x+9.Докажите ,что Р(Х)больше либо равно 0 для любых...

Question

Дан многочлен P(X)=2x квадрат -4x+9.Докажите ,что Р(Х)больше либо равно 0 для любых значений переменной х.(Полное решение)

Answer 1

P(X)=2x^2-4x+9 = 2(x-1)^2+7 >=7, т.к квадрат неотрицательный

Answer 2

I СПОСОБ

 

P(X) = 2x² - 4x + 9 ≥ 0 

Исследуем ф-цию P(X), сначала  найдем нули ф-ции:

          2x² - 4x + 9 = 0

          D = (-4)² - 4*2*9 = 16 - 72 =  - 56  < 0  ⇒  ф-ция P(X) ≠ 0  ∀ Х ∈ R.

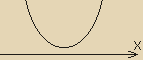
Значит график нигде не пересекает ось ОХ.

Коэффициент при старшем члене равен 2, т.е. он > 0   ⇒    ветви параболы направлены вверх.  Итак, график ф-ции  выглядит так  как показано на картинке  ⇒  P(X) >  0  ∀ Х ∈ R

 

II СПОСОБ

 

P(X) = 2x² - 4x + 9  =  2x² - 4x + 2 + 7  = 2(x² - 2х + 1) + 7  =  2(x - 1)² + 7 

 

 в данном выражении  (x - 1)² ≥ 0    ⇒    2(x - 1)²≥ 0   и   7  >   0     ⇒ 

  2(x - 1)² + 7 ≥ 0   ∀ Х ∈ R

                                                                                 

 

 

 

---