Пошаговое объяснение (мысли курсивом) :
1) Корень кубический из числа существует при любых действительных значениях Х. Преобразуем выражение под знаком радикала и получаем:
1) f(x) = (2-x)(x²-4x+1)= -x³ + 6x² - 9x + 2 - полином 3-ей степени.
2) f(x) - непрерывная, y(x)=∛f(x) - непрерывная.
Ответ: D(y) - Х∈(-∞;+∞) - интервал (область) определения функции.
2. Находим асимптоты функции.
а) Функция непрерывная, гладкая, разрывов -нет.
Ответ: Вертикальных асимптот - нет.
б) Наклонная асимптота по формуле: y = k*x+b.
![k= \lim_{x \to \infty}\frac{y(x)}{x}=\frac{\sqrt[3]{-x^3+6x^2-9x+2}}{x}=\\ = \lim_{x \to \infty}\sqrt[3]{-1+\frac{6}{x}-\frac{9}{x^2}+\frac{1}{x^3}}=\sqrt[3]{-1}=-1 k= \lim_{x \to \infty}\frac{y(x)}{x}=\frac{\sqrt[3]{-x^3+6x^2-9x+2}}{x}=\\ = \lim_{x \to \infty}\sqrt[3]{-1+\frac{6}{x}-\frac{9}{x^2}+\frac{1}{x^3}}=\sqrt[3]{-1}=-1](https://tex.z-dn.net/?f=k%3D%20%5Clim_%7Bx%20%5Cto%20%5Cinfty%7D%5Cfrac%7By%28x%29%7D%7Bx%7D%3D%5Cfrac%7B%5Csqrt%5B3%5D%7B-x%5E3%2B6x%5E2-9x%2B2%7D%7D%7Bx%7D%3D%5C%5C%20%3D%20%5Clim_%7Bx%20%5Cto%20%5Cinfty%7D%5Csqrt%5B3%5D%7B-1%2B%5Cfrac%7B6%7D%7Bx%7D-%5Cfrac%7B9%7D%7Bx%5E2%7D%2B%5Cfrac%7B1%7D%7Bx%5E3%7D%7D%3D%5Csqrt%5B3%5D%7B-1%7D%3D-1)
k = -1 - коэффициент наклона (запомним).
Хотя такой же ответ можно получить проще, зная что он равен пределу отношения членов с наибольшими показателями при Х.
![k= \lim_{x \to \infty}\frac{y(x)}{x}= \lim_{x \to \infty} \frac{\sqrt[3]{-x^3}}{x}= \lim_{x \to \infty}\frac{-x}{x}=-1 k= \lim_{x \to \infty}\frac{y(x)}{x}= \lim_{x \to \infty} \frac{\sqrt[3]{-x^3}}{x}= \lim_{x \to \infty}\frac{-x}{x}=-1](https://tex.z-dn.net/?f=k%3D%20%5Clim_%7Bx%20%5Cto%20%5Cinfty%7D%5Cfrac%7By%28x%29%7D%7Bx%7D%3D%20%5Clim_%7Bx%20%5Cto%20%5Cinfty%7D%20%5Cfrac%7B%5Csqrt%5B3%5D%7B-x%5E3%7D%7D%7Bx%7D%3D%20%5Clim_%7Bx%20%5Cto%20%5Cinfty%7D%5Cfrac%7B-x%7D%7Bx%7D%3D-1)
Находим значение сдвига по оси ОУ - b.
 - формула.
- формула.
Запишем формулу в раскрытом виде:
![b= \lim_{x \to \infty} [\sqrt[3]{-x^3+6x^2-9x+2}+x]} b= \lim_{x \to \infty} [\sqrt[3]{-x^3+6x^2-9x+2}+x]}](https://tex.z-dn.net/?f=b%3D%20%5Clim_%7Bx%20%5Cto%20%5Cinfty%7D%20%5B%5Csqrt%5B3%5D%7B-x%5E3%2B6x%5E2-9x%2B2%7D%2Bx%5D%7D)
Конечно можно найти решение через формулы сумму кубов, но ... мы пойдём другим путём.
Возвращаемся к функции под знаком радикала и найдём её нули. Функция третьего порядка и может быть (не обязательно) три нуля.
f(x) = (2-x)*(x²-4*x+1)=0.
2 - x = 0 и х₁ = 2 - результат из первой скобки.
Два других найдём решив квадратное уравнение.
x² - 4x + 1 = 0 - квадратное уравнение.
D = (-4)² - 4*1*1 = 12 - дискриминант. √D =√(2²*3) = 2√3.
Корни: x₂ = 2 - √3, x₃ = 2 + √3 - ещё два значения нуля функции f(x) под знаком радикала.
Основную функцию можно записать в виде:
Y(x) = ∛(x₂*x₁*x₃) = ∛(x₁-√3)(x₁)(x₁+√3).
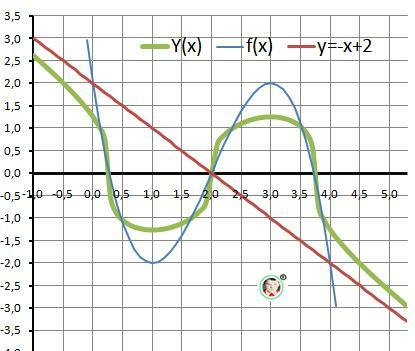
Из этого делаем вывод, что она симметрична относительно точки (2;0) и асимптота проходит через эту точку.
y = k*x+ b = 0 = - 1*2 + b
b = 2 - сдвиг по оси ОУ.
Можно записать:
y = - x+ 2 - уравнение касательной - ответ.
Рисунок с графиками только в помощь для наглядного понимания задачи.