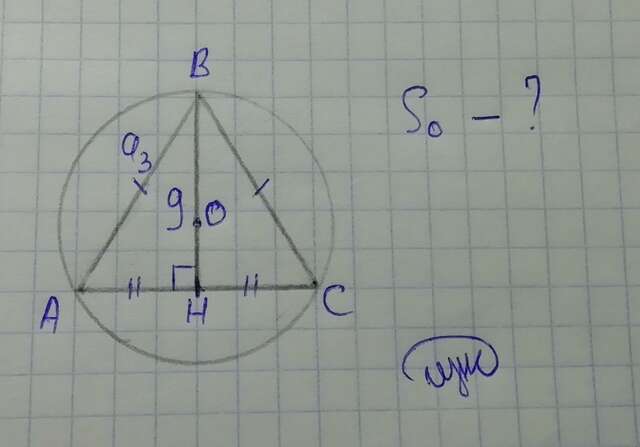
Рассмотрим правильный ΔABC
AH = AC/2 = AB/2 (в правильном треугольнике все стороны равны; высота правильного треугольника является его медианой, т. е. делит сторону треугольника на 2 равные части)
Рассмотрим ΔABH: AH = AB/2, BH = 9 см.
По теореме Пифагора
AB² = AH² + BH²

Воспользуемся формулой для стороны правильного треугольника
a₃ = R√3, где a₃ - сторона правильного треугольника, R - радиус описанной около него окружности
Подставляем
6√3 = R√3

Формула площади круга:
S = πR², где S - площадь круга, π - число Пи (≈ 3,14), R - радиус круга
Подставляем
S = π * 6² = 36π см²
Ответ: S = 36π см²