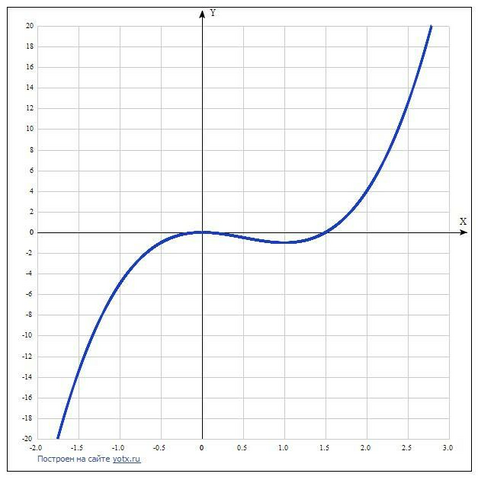
Дана функция F(x) =2x³-3x².
Полное исследование функций по схеме:
1. Область определения функции - ограничений нет, поэтому х ∈ Z.
2. Непрерывность функции, вертикальные асимптоты.
Разрывов функции нет - она непрерывна, асимптот нет.
3. Точки пересечения функции с осями координат.
- с осью Оу при х = 0 у = 0.
- с осью Оу при у = 0 надо решить уравнение 2x³-3x² = 0.
x²(2х - 3) = 0. Получаем 2 точки: х = 0 и х = 3/2.
4. Четность, нечетность - функция общего вида.
5. Периодичность - нет.
6. Промежутки возрастания, убывания, экстремумы функции.
Производная равна: y' = 6x² - 6x = 6x(x - 1) = 0.
Получаем 2 экстремума: х = 0 и х = 1.
Находим знаки производной на полученных промежутках.
x = -1 0 0,5 1 2
y' = 12 0 -1,5 0 12
.
Максимум в точке х = 0 (переход с + на -), у = 0,
минимум в точке х = 1 (переход с - на +).
Функция возрастает на промежутках (-∞; 0) и (1; +∞),
убывает на промежутке (0; 1).
7. Промежутки выпуклости, вогнутости, точки перегиба.
Вторая производная равна: y'' = 12x - 6 = 6(2x - 1) = 0.
Перегиб в точке х = 1/2.
Функция выпуклая на промежутке (-∞; (1/2) и вогнута ((1/2); +∞).
8. Наклонные асимптоты - нет.
9. Построение графика по точкам:
xy
-2.0-28
-1.5-13.5
-1.0-5
-0.5-1
00
0.5-0.5
1.0-1
1.50
2.04
2.512.5
3.027