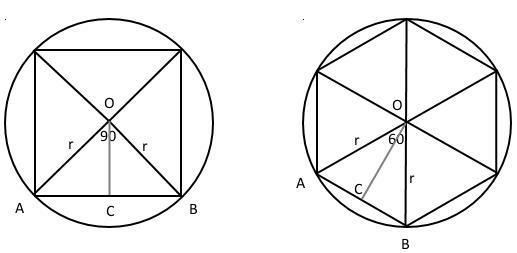
Чертим квадрат и шестиугольник, у обоих надо найти сторону AB, там получаются равнобедренные треугольники AOB, потому что AO и OB - радиусы r, у квадрата ∠AOB = 90°, потому что 360° всей окружности делятся на 4 равные части, у шестиугольника аналогично ∠AOB = 60°. Раз треугольники равнобедренные, то высоты OC делят являются медианами и биссектриссами углов AOB. Найдем AC у квадрата: r sin 45° = r √2/2; у шестиугольника: r sin 30° = r/2. Ну и отношение соответственно (r√2/2)/(r/2) = √2.