Ответ:
3:1
Пошаговое объяснение:
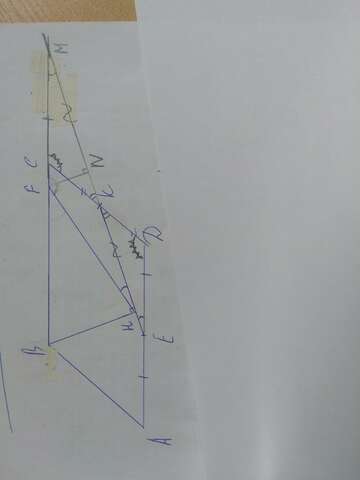
продливаем ЕК до пересечения с ВС . ЕК пересекает ВС в точке М
∠KED=∠CMK, как внутренние разн. при ЕD║СМ, где CD секущая.
так как угол ∠KED = ∠FHK из условия, следовательно ∠FHK = ∠СМК, и следовательно ΔHFM -равнобедренный.
так же ∠FDK=∠MCK и ∠EKD=∠CKM (как вертикальные углы)
сторона DK=KC по условию
⇒ΔEDK=ΔKCM ( по двум углам и стороне между ними)⇒СМ=ED
ED=АЕ; BC=AD=2AE=2ED
BM=3ED=3CM
опустим высоту FN в ΔHFM, высота является и медианой, так как треугольник равнобедренный HN=NM
так как FN⊥EM и BH⊥EM ⇒ BH║FN
по теореме фалеса BF=FM
BF=FM=3CM
FM=BF=BM/2=3CM/2
FC=FM-CM=3CM/2-2CM/2=CM/2
BF/FC= (3CM/2):(CM/2)=3:1