разберемся с множителями:
так как в первом множителе есть модуль, в котором линенйное уравнение, то в нем может быть 2 корня; Так как во втором множителе квадратное уравнение, то в нем может быть максимум 2 корня, следовательно максимальное значение корней может быть 4;
Разберемся с 1 множителем:
1) |x-2|-a-4=0;
при x>=2:
x-a-6=0;
x=a+6
т.к. x>=2, то a>=-4;
2) при x<2</p>
-x-a-2=0
x=-(a+2);
т.к. x<2, то a>-4;
из этих двух случаев получаем: a>-4 (при a=-4, данный множитель имеет один кррень);
Рассмотрим второй множитель:
x^2-4x+a+6;
D=16-4(a+6)=-8-4a=-4(a+2);
т.к. D>0, то a<-2, тогда корни будут:</p>
x1=2+кв.корень(-(a+2)) (четверка вынесется за корень, я не стал это расписывать);
x2=2-кв.корень(-(a+2));
получаем: a приеадлежит (-4;-2);
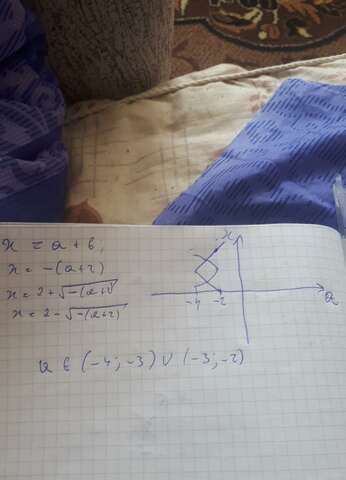
Исключим вариант, где первый и второй множитель дают одинаковые корни - это лучше всего показать графически:
Построим графики уравнений:
x=a+6;
x=-(a+2);
x=2+кв.корень(-(a+2));
x=2-кв.корень(-(a+2)),
на отрезке: a приеадлежит (-4;-2);
(смотреть рисунок)
Заметим, что при a=-3 графики пересекаются, значит при данном значении a всего имеем 2 корня;
В итоге имеем:
a принадлежит (-4;-3) U (-3;-2)