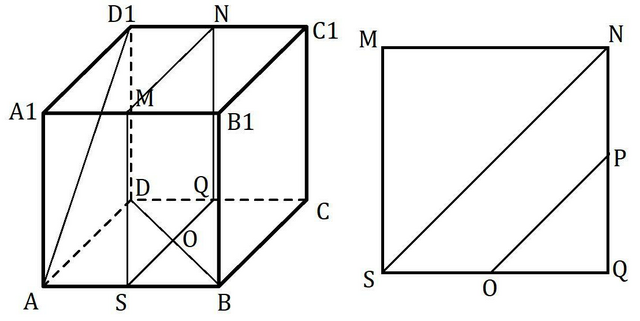
Смотри на картинку.
S∈AB; AS=SB
Q∈DC; DQ=QC
M∈A₁B₁; A₁M=MB₁
Проведём плоскость α через точки S, Q, M это плоскость параллельна (AA₁D₁) по признаку. α∩D₁C₁=N; A₁D₁║MN --> D₁N=NC₁ (по теореме Фалеса).
В общем имеем что квадрат AA₁D₁D равен квадрату SMNQ и они параллельны. Значит SN║AD₁ Напомню, что угол между прямыми сохраняется при параллельном переносе. SQ∩DB=O; SO=OQ как соответственные средние линии равных треугольников (ΔAOD и ΔBDC).
Смотри рисунок.
Через точку O проведём прямую OP (OP║SN), из построение следует, что QP=PN (по теореме Фалеса). Ещё раз угол при параллельном переносе прямых сохраняется.
В общем у нас есть ΔDOP и нам надо найти ∠DOP.
Скажем, что сторона куба равна а.
DB=a*√2 --> DO=a*√2/2
SN=a*√2 --> OP=a*√2/2
P-середина квадрата DD₁C₁C т.к. QN║DD₁ и DQ=QC, и QP=PC.
Значит P∈DC₁ и DP=PC₁
DC₁=a*√2 --> DP=a*√2/2
Получается ΔDOP - равносторонний и угол 60°.
Ответ: 60°.