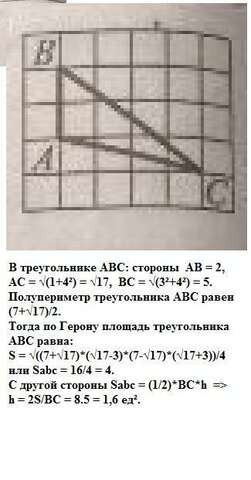
В треугольнике АВС стороны равны:
АВ = 2,
АС = √(1+4²) = √17 (по Пифагору),
ВС = √(3²+4²) = 5 (тоже по Пифагору.
Полупериметр треугольника АВС равен (7+√17)/2 ед.
Тогда по Герону площадь треугольника АВС равна:
S = √((7+√17)*(√17-3)*(7-√17)*(√17+3))/4 или
Sabc = 16/4 = 4 ед².
С другой стороны Sabc = (1/2)*BC*h =>
h = 2S/ВС = 8/5 = 1,6 ед.
Ответ: высота, опущенная на сторону ВС, равна 1,6 ед.
P.S. для сравнения:
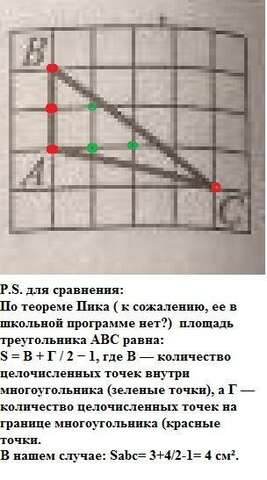
По теореме Пика ( к сожалению, ее в школьной программе нет?) площадь треугольника АВС равна:
S = В + Г / 2 − 1, где В — количество целочисленных точек внутри многоугольника (зеленые точки), а Г — количество целочисленных точек на границе многоугольника (красные точки.
В нашем случае: Sabc= 3+4/2-1= 4 см².