Ответ:
Пошаговое объяснение:
ОДЗ x²-x+8>0 d=1-4*8=-31 ⇒ так как коэффициент при х² а=1>0 и дискриминант<0 то ОДЗ x∈R</p>
lg(x²-x+8)>1
lg(x²-x+8)>lg10¹
lg(x²-x+8)>lg10
x²-x+8>10 решим методом интервалов
найдем корни
x²-x-2>0 ; d=1+8=9; x₁₋₂=(1±√9)/2=(1±3)/2={-1;2}
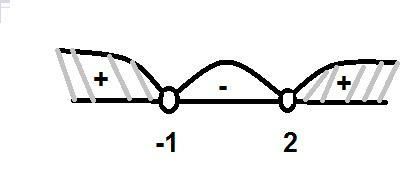
нанесем корни на числовую прямую, определим знак неравенства на каждом интервале, для этого из каждого интервала можно взять любое число и подставить в выражение x²-x-2 знак выражения отмечаем на каждом интервале см. рисунок
так как неравенство >0 выбираем положительные интервалы и записываем в ответ
x∈(-∞;-1)∪(2;+∞)