С помощью циркуля и линейки постройте угол ABC равный углу PNKдам 50 баллов, пожалуйста...

Question

С помощью циркуля и линейки постройте угол ABC равный углу PNKдам 50 баллов, пожалуйста решите только!​

Answer 1

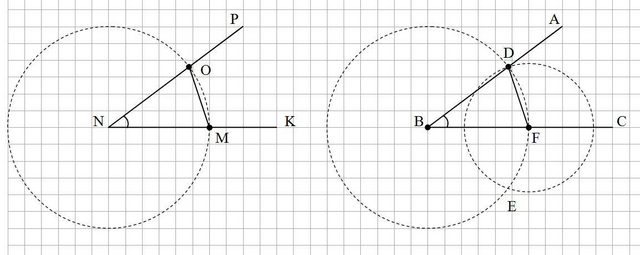
Дано: ∠PNK; [BC)

Построить: ∠ABC = ∠PNK  

1. Обозначим на луче NK произвольную точку М.

2. Построим с помощью циркуля окружность с центром в точке N и радиусом, равным NM.

3. Построенная окружность пересечет луч NP в точке О.

4. Строим окружность с тем же радиусом и с центром в точке В, которая пересечет луч ВС в точке F.

5. Измерим циркулем расстояние ОМ.

6. Строим окружность с центром в точке F и радиусом, равным ОМ, которая пересечет первую построенную окружность в двух точках.

7. Выберем любую из них, например точку D, и построим луч ВD.

Построенный угол будет равен исходному углу PNK.

-------------------------------------

Докажем, что ∠АВС = ∠PNK

Так как окружности с центром в точке N и с центром в точке В имеют равные радиусы, то:

                NO = NM = BF = BD

Отрезок ОМ равен отрезку FD по построению.

Таким образом, ΔONM = ΔFBD по трем сторонам.

Следовательно,  ∠АВС = ∠PNK

---

Answer 2

Пусть дан угол с вершиной в точке О (верхний рисунок).

Начертим прямую а. Отметим на ней произвольную точку O'.

Проведем окружность произвольного радиуса с центром в точке О. Эта окружность пересечет стороны данного угла в точках А и В.

Не меняя раствор циркуля, проведем окружность с центром в точке O'. Она пересечет прямую а в точке B'.

Проведем окружность с центром в точке В, радиусом АВ.

Не меняя раствор циркуля, проведем окружность с центром в точке B'.

Она пересечет первую окружность в точке A'.

Проведем луч O'A'.

Угол A'O'B' - искомый.

---