ПОМОГИИИИИИИИИИИТЕЕЕЕ 7 КЛАААААССДАЮ 40 БАЛЛОВ !!!!!!!!!!СРОЧНО!!!!!!!!!!!!!На...

Дан 1 ответ

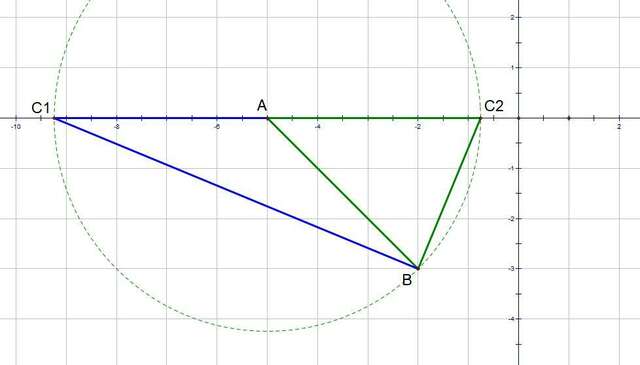
Точка C лежит на оси абсцисс ⇔ вторая координата равна нулю.

То есть b = 0

ΔABC - р/б ⇒ AB = AC ⇒ длины векторов AB и AC равны:

$|\overline{AB}|=|\overline{AC}|$

Найдём длину вектора AB по формуле:

$|\overline{AB}|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=\sqrt{(-2-(-5))^2+(-3-0)^2}=\\ =\sqrt{3^2+(-3)^2}=\sqrt{9+9}=\sqrt{9*2}=3\sqrt{2}$

И выразим длину вектора AC:

$|\overline{AC}|=\sqrt{a-(-5))^2+(0-0)^2}=\sqrt{(a+5)^2}=|a+5|$

Так как AB=AC, можно составить уравнение:

$|a+5|=3\sqrt{2}\\ \\ \left \{ {{a+5=3\sqrt{2}} \atop {a\geq-5}} \right. \\ \left \{ {{a+5=-3\sqrt{2}} \atop {a<-5}} \right. \\\\\\ \left \{ {{a=3\sqrt{2}-5} \atop {a\geq-5}} \right. \\ \left \{ {{a=-3\sqrt{2}-5} \atop {a<-5}} \right.$

Обе системы дают по одному корню:

a₁ = 3√2 - 5

a₂ = -3√2 - 5

Нужно найти значение выражения 3a - b. Так как значений a несколько, то и ответов будет несколько:

3a₁ - b = 3(3√2 - 5) - 0 = 9√3 - 15

3a₂ - b = 3(-3√2 - 5) - 0 = -15 - 9√3

Ответ: -15 - 9√3; 9√3 - 15

* во вложении построены два случая: ΔABC₁ и ΔABC₂

Хуqожнuк_zn (25.4k баллов) 01 Июнь, 20

ПОМОГИИИИИИИИИИИТЕЕЕЕ 7 КЛАААААССДАЮ 40 БАЛЛОВ !!!!!!!!!!СРОЧНО!!!!!!!!!!!!!**...