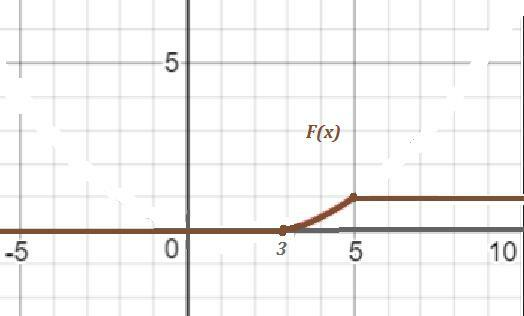
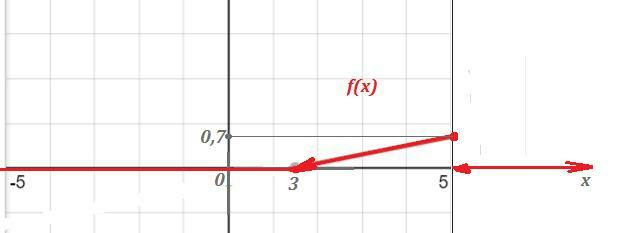
5\; .\end{array}\right\\\\\\1)\; \; f(x)=F'(X)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\a(2x-3)\; ,\; 35\; .\end{array}\right\\\\\\2)\; \; \int a\cdot (2x-3)dx=a\cdot (2\cdot \frac{x^2}{2}-3x)+C=a\cdot (x^2-3x)+C\\\\\\3)\; \; \int \limits _{-\infty }^{+\infty }\; f(x)\, dx=1\; \; ,\; \; f(x)\geq 0\; \; \Rightarrow " alt="F(X)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\a(x^2-3x)\; ,\; 35\; .\end{array}\right\\\\\\1)\; \; f(x)=F'(X)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\a(2x-3)\; ,\; 35\; .\end{array}\right\\\\\\2)\; \; \int a\cdot (2x-3)dx=a\cdot (2\cdot \frac{x^2}{2}-3x)+C=a\cdot (x^2-3x)+C\\\\\\3)\; \; \int \limits _{-\infty }^{+\infty }\; f(x)\, dx=1\; \; ,\; \; f(x)\geq 0\; \; \Rightarrow " align="absmiddle" class="latex-formula">
5\; .\end{array}\right\\\\\\1)\; \; f(x)=F'(X)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\a(2x-3)\; ,\; 35\; .\end{array}\right\\\\\\2)\; \; \int a\cdot (2x-3)dx=a\cdot (2\cdot \frac{x^2}{2}-3x)+C=a\cdot (x^2-3x)+C\\\\\\3)\; \; \int \limits _{-\infty }^{+\infty }\; f(x)\, dx=1\; \; ,\; \; f(x)\geq 0\; \; \Rightarrow " alt="F(X)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\a(x^2-3x)\; ,\; 35\; .\end{array}\right\\\\\\1)\; \; f(x)=F'(X)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\a(2x-3)\; ,\; 35\; .\end{array}\right\\\\\\2)\; \; \int a\cdot (2x-3)dx=a\cdot (2\cdot \frac{x^2}{2}-3x)+C=a\cdot (x^2-3x)+C\\\\\\3)\; \; \int \limits _{-\infty }^{+\infty }\; f(x)\, dx=1\; \; ,\; \; f(x)\geq 0\; \; \Rightarrow " align="absmiddle" class="latex-formula">
 5\; .\end{array}\right \; \; ,\; \; f(x)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\0,1(2x-3)\; ,\; 35\; .\end{array}\right\\\\\\0,1(2x-3)\geq 0\; \; pri\; \; 35\; .\end{array}\right \; \; ,\; \; f(x)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\0,1(2x-3)\; ,\; 35\; .\end{array}\right\\\\\\0,1(2x-3)\geq 0\; \; pri\; \; 3
5\; .\end{array}\right \; \; ,\; \; f(x)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\0,1(2x-3)\; ,\; 35\; .\end{array}\right\\\\\\0,1(2x-3)\geq 0\; \; pri\; \; 35\; .\end{array}\right \; \; ,\; \; f(x)=\left\{\begin{array}{l}0\; ,\; \; \; x\leq 3\; ,\\0,1(2x-3)\; ,\; 35\; .\end{array}\right\\\\\\0,1(2x-3)\geq 0\; \; pri\; \; 3