У рівнобедренному трикутнику DEF DE=EF. висота DH утворює з основою DF кут, який дорівнює...

Question

У рівнобедренному трикутнику DEF DE=EF. висота DH утворює з основою DF кут, який дорівнює 15 градусів. Знайдіть DE, якщо DH=4 см.

Answer 1

Все легко, только не просите рисовать. Вот сначала разберемся с углами. т.к. ДН- высота, то ДНF=ДНЕ=90°, Т.к. ∠НДF =15°,   в ΔНДF, то ∠НFД =75°, тогда и ∠ЕДF=75°  как углы при основании равнобедренного ΔДЕF. Но тогда в ΔДЕН ∠ Н равен 90°, ∠ ЕДН=75°-15°=60°, и на долю ∠ДЕН приходится 30°. Значит, катет ДН =4 см в два раза меньше гипотенузы ДЕ, т.е. 8см.

ОТвте 8 см

Answer 2

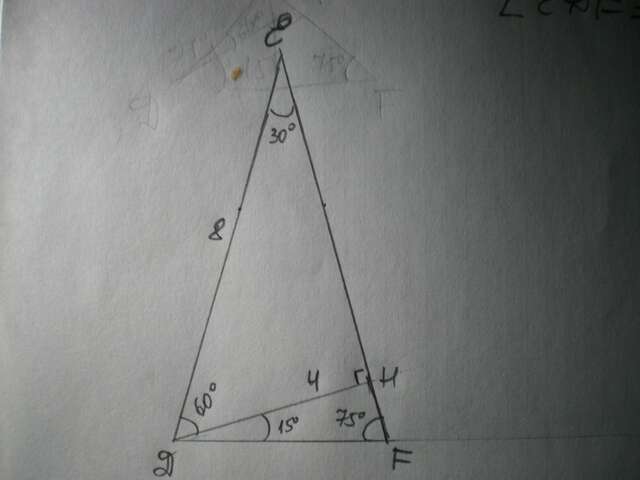
Дано: Δ DEF - рівнобедрений, DE=EF, висота DH, DH=4 см, ∠НDF=15°. Знайти DE.

ΔDНF - прямокутний, ∡НDF=15°, ∠DFН=90-15=75°.

∠D=∠Н=75°.

ΔDЕН - прямокутний, ∠ЕDН=75-15=60°, тоді ∠Е=90-60=30°.

Проти кута 30° лежить катет DН=4 см, отже, DЕ=2DН=4*2=8 см.

Відповідь: 8 см.

---