Про невырожденный треугольник ABC известно, что AB=3.5, AC=2.4, а длина стороны BC...

Question

Про невырожденный треугольник ABC известно, что AB=3.5, AC=2.4, а длина стороны BC выражается целым числом n. Чему может быть равно n? Если ответов несколько, введите их в порядке возрастания через пробел.

Answer 1

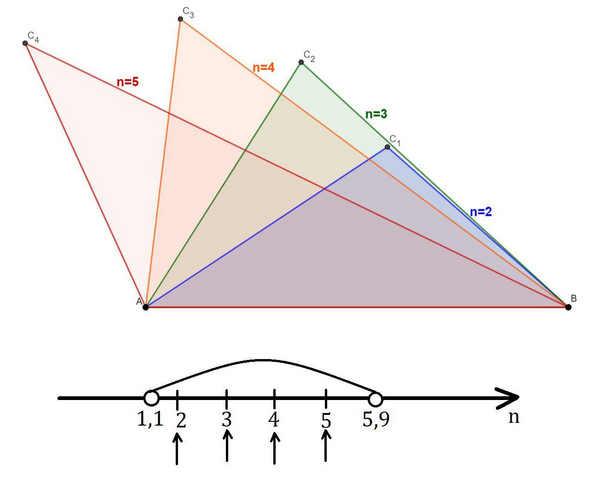
Сумма двух сторон сторон треугольника всегда больше третьей (неравенство треугольника). Таким образом, получим:

BC\\AB+BC>AC\\AC+BC>AB\end{matrix} \quad \begin{Bmatrix}3,\!5+2,\!4>n\\3,\!5+n>2,\!4\\2,\!4+n>3,\!5\end{matrix}" alt="\begin{Bmatrix}AB+AC>BC\\AB+BC>AC\\AC+BC>AB\end{matrix} \quad \begin{Bmatrix}3,\!5+2,\!4>n\\3,\!5+n>2,\!4\\2,\!4+n>3,\!5\end{matrix}" align="absmiddle" class="latex-formula">

-1,\!1\\n>1,\!1\end{matrix}\quad 1,\!1-1,\!1\\n>1,\!1\end{matrix}\quad 1,\!1

Раз n - целое, то n={2;3;4;5}

Ответ: 2, 3, 4 или 5.

---