2\end{matrix}" alt="f(x)=\begin{Bmatrix}10+3x,x<-2\\x^2,-2\le x\le 2\\10-3x,x>2\end{matrix}" align="absmiddle" class="latex-formula">
2\end{matrix}" alt="f(x)=\begin{Bmatrix}10+3x,x<-2\\x^2,-2\le x\le 2\\10-3x,x>2\end{matrix}" align="absmiddle" class="latex-formula">
Сначала построим уравнение прямых.
Прямые можно построить по двум точкам, в конце нас интересует, когда функция положительная, поэтому первой точкой будет точка при абсциссе которой функция обращается в ноль, а второй точкой будет граница промежутка на котором определена функция.
1. f(x)=10+3x,x<-2</p>

2. f(x)=10-3x,x>2

Рассмотрим функцию на промежутке -2 ≤ x ≤ 2.
f(x)=x^2
Это парабола ветви которой направлены вверх.
Найдём её точки по той же схеме, что и предыдущие.

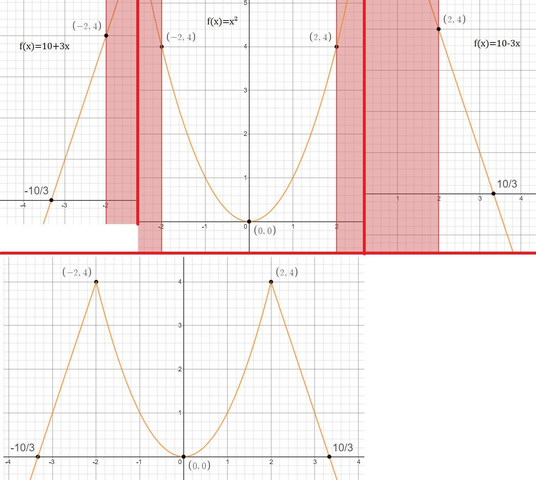
Теперь построим отдельно графики функции с их ограничениями, а затем совместим всё в один. Уже по точкам, что мы нашли видно, что значение функции совпадает в граница, поэтому это будет непрерывная функция.
Смотри вниз.
Про вопрос:
нас интересуют значения х, по точкам мы можем с лёгкостью их определить, но стоит заметить, что нас интересует когда функция положительная, то если случаи когда она равна нулю нас не интересуют, смотря на ординаты точек мы можем определить, когда функция положительная.
Ответ: x∈(-2;0)∪(0;2).