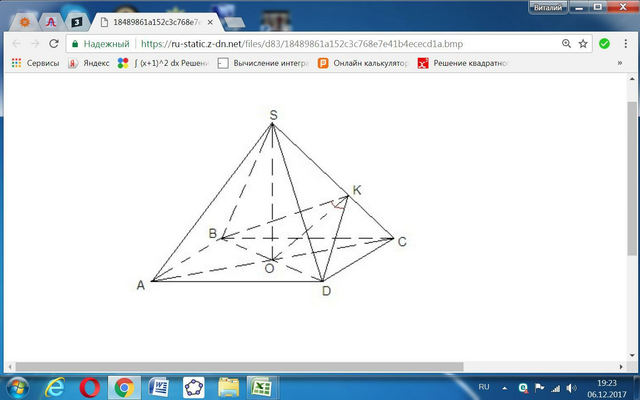
Рассмотрим треугольник ВКД. Угол ВКД и есть угол альфа.
Диагонали d = АС = ВД = а√2.
Высота ОK = (d/2)/tg(α/2) = (а√2/2)/(tg(α/2)).
Теперь перейдём к треугольнику ОSC. Пусть угол SCО - это β.
sin β = OK/OC = (а√2/2)/(tg(α/2))/((а√2/2) = 1/tg (α/2).
tg β = sin β/√(1 - sin²β) = 1/√(tg² (α/2) - 1).
Отсюда находим высоту пирамиды:
Н = ОС*tg (α/2) = a√2/(2√(tg² (α/2) - 1)).
Объём пирамиды равен:
V = (1/3)SoH = (1/3)a²*(a√2/(2√(tg² (α/2) - 1))) = a³√2/(6√(tg² (α/2) - 1)).