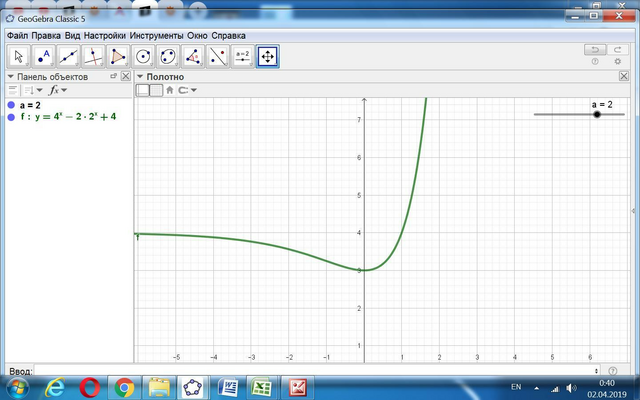
Дана функция 
Её можно дать так: y = (2^x)²-a*2^x + 4. Заменим 2^x = m.
y = m² - am + 4.
Производную приравняем нулю: y' = 2m - a = 0. a = 2m.
Полученное значение подставим в выражение функции, которая должна быть равна 3.
m² -2m*m + 4 = 3.
Отсюда получаем m² = 1, тогда m = +-1. Отрицательное значение неприемлемо (2 в любой степени не может быть отрицательным).
Обратная замена: 2^x = 1 или 2^x = 2^0.
Найдена абсцисса,в которой функция равна 3.
Теперь находим значение а = 2m = 2*1 = 2.
Уравнение функции, минимум которой равен 3: