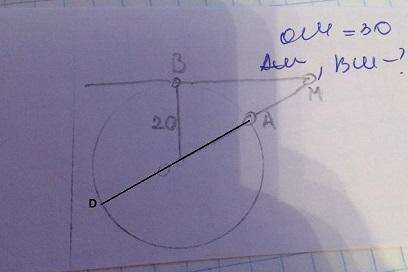
АМ = ОМ - ОА = ОМ - ОВ = 30 - 20 = 10 ед. (ОА=ОВ - радиусы).
Проведем МО до второго пересечения с окружностью в точке D.
DА= - диаметр окружности. DМ= DA+AM =2*R +АМ=50 ед.
По теореме о касательной и секущей: ВМ² = DМ²*AМ².
ВМ = √(50*10) = √(30*10) = 10√5 ед.
Ответ: АМ = 10ед. ВМ = 10√5 ед.
Второй вариант:
Из прямоугольного треугольника ОВМ:
ВМ=√(ОМ²-ОВ²) = √30²-20²) = 10√5 ед.
АМ = ОМ - ОА = 10 ед.
Ответ: АМ = 10ед. ВМ = 10√5 ед.