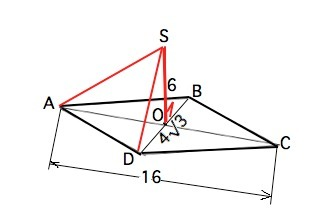
Через точку О пересечения диагоналей ромба ABCD проведена прямая OS, перпендикулярная к плоскости ромба, причем OS=6 см, AC=16 см, BD=4√3. Найдите расстояние от точки S до вершин ромба. ( Условие должно быть таким, т.к. АS- расстояние от S до вершины А и С ромба. В условии явно опечатка).
SO перпендикулярен плоскости ромба, значит, перпендикулярен любой прямой, проходящей в плоскости ромба через О.
АО=ВО=16:2=8
ВО=DО=2√3
Из прямоугольных ∆ SOA и ∆ SOD по т.Пифагора
SA=√(SO*+AO*)=√100=10 см
SD=√(AO*+DO*)=√48=4√3 см
SC=SA=10; SD=SB=4√3 см