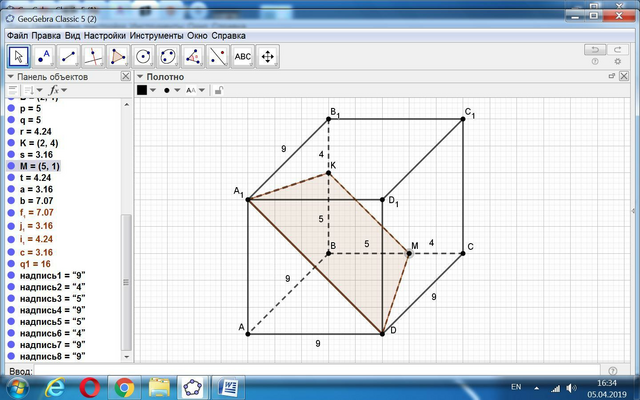
10. Отрезок КМ как лежащий в параллельной плоскости параллелен диагонали А1Д.
В сечении имеем равнобокую трапецию А1КМД.
Её стороны легко определяются. А1Д = 9√2, КМ 5√2,
А1К = МД = √(9² + 4²) = √(81 + 16) = √97.
Находим высоту Н трапеции:
Н = √((√97)² - ((9√2 - 5√2)/2)² = √(97 - 8) = √89.
Получаем ответ: S(A1KMD) = (((5 + 9)√2)/2)*√89 = 7√178 кв.ед.
11.а. Приведём к общему знаменателю.

Обе части умножим на х + 6:
x²+6x + 20 ≥ 6x + 36,
x² ≥ 16. Отсюда х ≥ 4 и х ≤ -4.
Так как дробь должна быть положительна, то знаки числителя и знаменателя должны совпадать. Числитель левее и правее точек х = -4 и х = 4 положителен (по свойству параболы).
Отсюда получаем: х ∈ (-6; -4] ∪ [4; +∞).
11.б. Примем выражение под корнем за t: t + (1/t) ≥ 5/2.
2t² + 2 ≥ 5t. Получили неравенство 2t² - 5t + 2 ≥ 0.
Находим нули: 2t² - 5t + 2 = 0. Д = 25-4*2*2 = 9. х=(5 ± 3)/4 = 2 и 1/2.
Обратная замена: t² = x + 4,2. 4 = x + 4,2, x = 4 - 4,2 = -0,2,
1/4 = x + 4,2, x = (1/4) - 4,2 = -79/20 = -3,95.
Ответ: х ∈ [-0,2; +∞) ∪ (-4,2; -3,95].
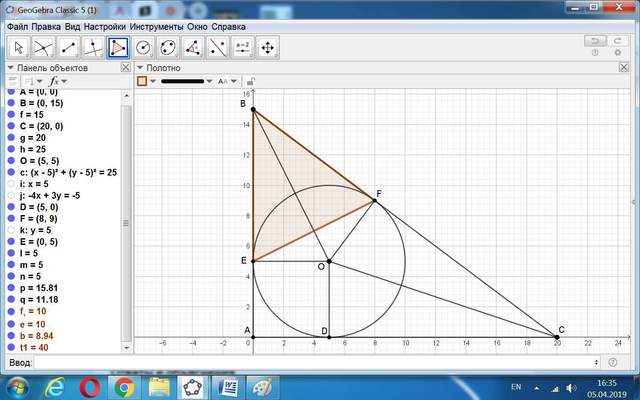
12. tg(C/2) = 5/15 = 1/3. tgC = (2*(1/3))/(1-(1/9)) = 3/4.
BE = AC*tgC - R = 20*(3/4) - 5 = 15 - 5 = 10. tg(B/2) = 5/10 = 1/2.
cos(B/2) = 10/5√5 = 2/√5.
BK = 10*cos(B/2) = 10*(2/√5) = 4√5.
sin(B/2) = √(1 - (4/5)) = 1/√5.
KE = 10*sin(B/2) = 10*(1/√5) = 2√5.
S = 2*(1/2)*2√5)*4√5 = 40.