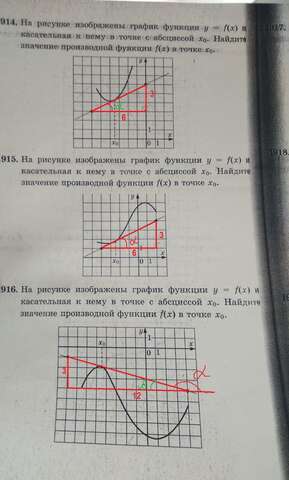
Производная в точке равна тангенсу угла наклона касательной: f'(x₀)=tgα
То есть достраиваем до прямоугольного треугольника, и находим тангенс, как отношение противолежащего катета к прилежащему
№1914
f'(x₀)=tgα=3/6=0,5. Ответ: 0,5
№1915
f'(x₀)=tgα=3/6=0,5. Ответ: 0,5
№1916
В этом номере чуть по-другому:
угол наклона прямой-это угол между самой прямой и ПОЛОЖИТЕЛЬНЫМ направлением оси Х.
В этой задаче угол наклона будет тупой, поэтому чтобы воспользоваться нашим правилом (а точнее геометрическим смыслом производной), нужно найти тангенс смежного с ним угла:
tgβ=3/12=0.25
Так как β=180°-α, то формуле приведения из тригонометрии:
tgβ=tg(180°-α)=-tgα=0.25, тогда
tgα=-0.25
Ответ: -0,25
P.S.
Можно просто запомнить: если касательная наклонена под острым углом, то тангенс (а значит и производная) будет положительный.
Если касательная наклонена под тупым углом, то тангенс будет отрицательным!