Ответ: 12
Объяснение:
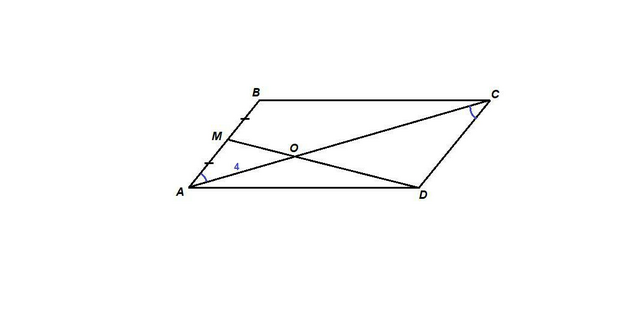
∠MAO = ∠DCO как накрест лежащие при пересечении параллельных прямых АВ и CD секущей АС,
∠МОА = ∠DOC как вертикальные, значит
ΔМОА подобен ΔDOC по двум углам.

Так как M середина стороны АВ, а противолежащие стороны в параллелограмме равны, то

OC = 2 · AO = 2 · 4 = 8
AC = AO + OC = 4 + 8 = 12