2. Не выполняя построения, найдите координаты точек пересечения графика функции y = 2x² и прямой:
a) y = 200
b) y = 50x
Решение:
a) Подставим y = 200 в заданную функцию
200 = 2x² ⇔ x² = 100 ⇔ x = ± 10
Координаты точек пересечения: (±10; 200).
b) Аналогично подставляем y = 50x в заданную функцию
50x = 2x² ⇔ 50x - 2x² = 0 ⇔ 2x (25 - x) = 0
Произведение равно нулю, если хотя бы один из множителей равен 0.
x = 0 ⇔ y = 0
25 - x = 0 ⇔ x = 25 и y = 50 * 25 = 1250.
Координаты точек пересечения: (0;0), (25;1250).
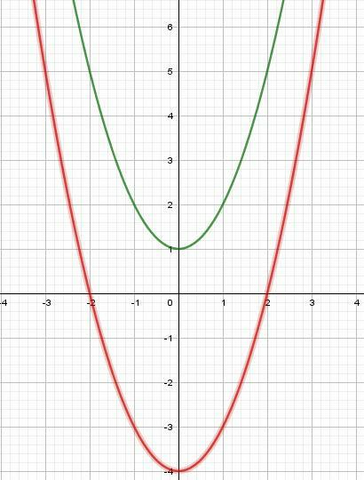
Постройте графики функций: y = x² + 1; y = x² - 4
y = x² + 1 преобразована из графика функции y = x² смещением на 1 ед. вверх, а у = х² - 4 из графика функции y = x² - 4 смещением на 4 ед. вниз.