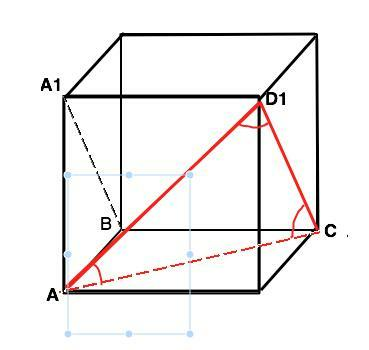
Ответ:60°
Объяснение:
А1В и АС лежат в разных плоскостях и не имеют общих точек. Они – скрещивающиеся.
Чтобы найти угол между скрещивающимися прямыми, нужно: Провести прямую, параллельную одной из двух скрещивающихся прямых так, чтобы она пересекала вторую прямую. При этом получатся пересекающиеся прямые. Угол между ними равен углу между исходными скрещивающимися.
СD1 ║ BA1 и пересекает АС в т.С. Если провести диагональ АD1 в грани АА1D1D, получим треугольник АD1С, все стороны которого равны между собой ( т.к. диагонали равных квадратов равны). Следовательно. углы ∆ АСD1 равны, их градусная мера 180°:3=60°.
Градусная мера угла между прямыми ВА1 и АС равна 60°.