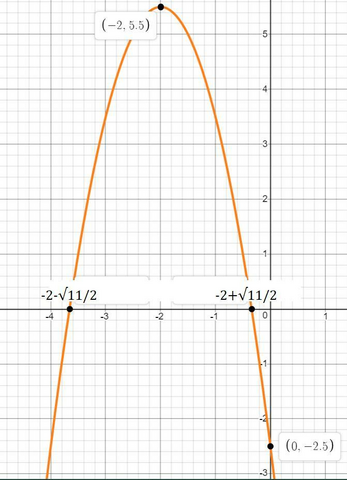
Я выделю полный квадрат и построю график функции переносом параболы.
Таким образом график это функции выглядит как график функции -2x^2, только он сдвинут на 2 влево и поднят на 5,5 вверх, соответственно координаты вершины (-2;5.5)
Осталось найти только точки пересечения с осями координат.
(-2.5;0)\\-2(x+2)^2+5,5=0;\\x+2=б\sqrt{\frac{11}{4}}\\x=\frac{-4б\sqrt{11}}{2}" alt="y(0)=-2*0^2-8*0-2,5=-2,5=>(-2.5;0)\\-2(x+2)^2+5,5=0;\\x+2=б\sqrt{\frac{11}{4}}\\x=\frac{-4б\sqrt{11}}{2}" align="absmiddle" class="latex-formula">
Последнее это соответственно нули функции.
Теперь можем строить.
