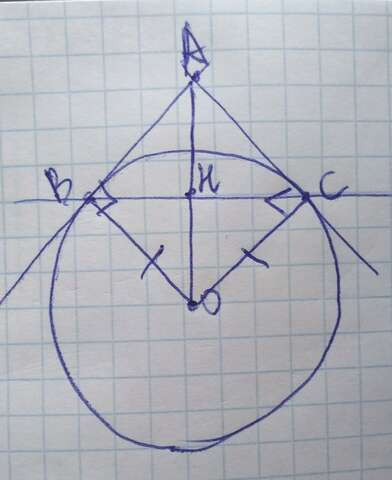
Так как А и О симметричны, значит, проведя линию ВС, точки А и О окажутся по разные стороны, но на одинаковом расстоянии от прямой ВС.
Так как радиус, проведенный в точку касания, образует с касательной угол 90°
А в четырехугольнике сумма углов равна 360°
У нас получилось 2 треугольника ВАС и ВОС
Проведем высоты ОН и АН к стороне ВС, высоты равны
Значит, по катету и гипотенузе равны треугольники ОСН и ВОН (т.к. треугольник равнобедренный, потому что ВО=ОС(радиусы одной окружности), а значит, ОН еще и медиана)
Так же и с треугольника ми ВАН и АНС
АВ =АС (как отрезки касательных), АН-медиана
Значит, треугольники ВАН и АНС равны по катету и гипотенузе
Рассматривая треугольники СНО и АНС можно сказать, что они так же равны по двум сторонам и углу между ними (НО=АН, НС-общая)
И так же с треугольниками ВАН и ВНО, они тоже равны по двум сторонам и углу между ними
Значит, ВА=АС=ВО=ОС, значит, АВОС-ромб
Так как углы АВО и АСО =90°
То и углы ВАС и ВОС равны по 90°
В сумме все дадут 360
Угол ВАС равен 90°