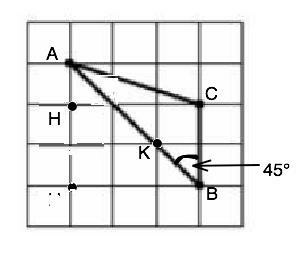
На клетчатой бумаге с размером клетки √5•√5 изображён треугольник. Найдите радиус его описанной окружности.
Ответ:5 (ед. длины)
Объяснение:
Обозначим вершины треугольника А, В, С. Любую точку на большей стороне, проходящую через вершину клетки, – буквой К. Сторона АВ угла СВА содержит диагональ квадрата, которая является биссектрисой прямого угла, следовательно, угол СВА=45°.
Обозначим т.Н вершину клетки ниже т.А.
Из ∆ АНС по т.Пифагора АС=√( AH²+HC²)=√((3√5)²+√5²)=5√2. По т.синусов 2R=AC/sin45°=5√2:(√2/2)==10 ⇒ R=5