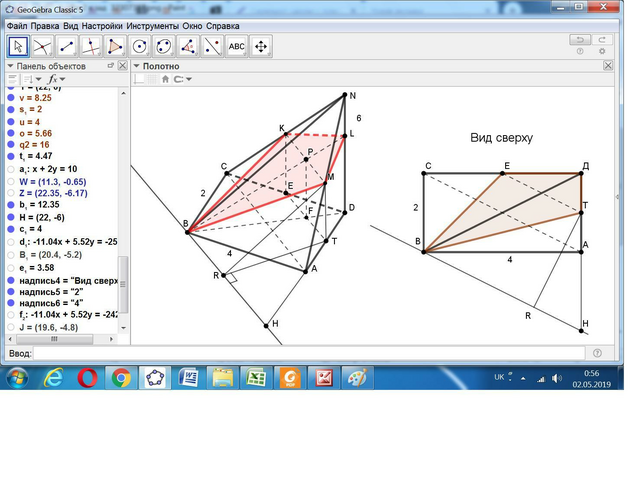
В сечении получаем четырёхугольник BKLM.
Точки K и M на основании задания расположены на расстоянии 6/2 = 3 ед. от плоскости основания.
Поэтому отрезок KM параллелен основанию.
Точка Р пересечения отрезков KM и BL, лежащих в плоскости сечения, тоже находится на расстоянии 3 ед. от основания.
Проекция отрезка BL на основание - это диагональ BD прямоугольника основания. Треугольники BPF и BLD подобны. Отрезок BF по построению равен (3/4)BD.
Отсюда находим длину отрезка LD.
LD = PF/(3/4) = 3/(3/4) =4 ед.
Получаем первый ответ: BL = √(2² + 4² + 4²) = √36 = 6 ед.
Проведём прямую ВН параллельно KM - это линия пересечения секущей плоскости и плоскости основания пирамиды. Продлим сторону AD до пересечения с ВН.
По свойству полученного параллелограмма ВСАН отрезок АН = ВС = 3 ед. Длина ТН = (2/2) + 3 = 4 ед.
Угол Н равен углу ВСА.
Его синус равен 4/√(2² + 4²) = 4/√20 = 4/(2√5) = 2/√5.
Отсюда находим: TR = TH*sin H = 3* (2/√5) = 6/√5.
Двугранный угол между секущей плоскостью и основанием равен плоскому углу, полученному при пересечении двух плоскостей третьей, проведенной перпендикулярно их линии пересечения. Это угол MRT.
Получаем второй ответ:
∠MRT = arctg MT/TR = arc tg(3/(6√5) arctg (√5/2) =
= arc tg 1,118034 = 0,841 радиан или 48,19 градуса.
Находим длину наклонной MR = √(MT² + TR²) = √(9 + (36/5)) = 9/√5.
Отсюда косинус угла MRT равен:
cos (MRT) = cos φ = TR/MR = (6/√5)/(9/√5) = 2/3.
Теперь определяем площадь проекции сечения на основание как площадь основания минус площади двух треугольников.
So = 2*4 - (1/2)*1*4 - (1/2)*2*2 = 8 - 2 - 2 = 4.
Получаем третий ответ: Sсеч = So/cos φ = 4/(2/3) = 6 кв.ед.