Из точки к окружности радиусом 15 проведены касательная и секущая. Точка A — точка...

Question

Из точки к окружности радиусом 15 проведены касательная и секущая. Точка A — точка касания. Секущая проходит через центр окружности и пересекает ее в сначала в точке K , а затем в точкеE , CK=10. Найдите AC . Найдите AE . В ответ запишите длину отрезка AE , деленную на корень из 5.

Answer 1

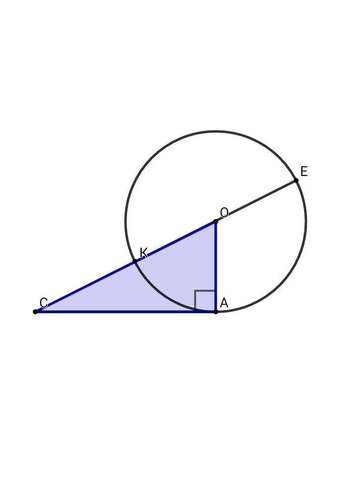
▪КО = ОЕ = АО = 15

СО = СК + КО = 10 + 15 = 25

▪Радиус, проведённый в точку касания касательной и окружности, перпендикулярен касательной.

В прям.тр.СОА: по т.Пифагора

АС^2 = СО^2 - АО^2 = 25^2 - 15^2 = 625 - 225 = 400 , АС = 20

▪СЕ = СО + ОЕ = 25 + 15 = 40

cosC = AC/CO = 20/25 = 4/5

По т.косинусов:

АЕ^2 = 40^2 + 20^2 - 2•40•20•(4/5)

АЕ^2 = 1600 + 400 - 1280 = 720

АЕ = 12V(5)

ОТВЕТ: 20 ; 12

---