Площадь ромба ABCD=768, DM-медиана треугольника АВD, MD=BD =20.Найдите AD

Ответ: 39,68

Пошаговое объяснение:

Ну, для меня лично эта медиана вводит в заблуждение, так как для решения мне понадобилось лишь знать одну из диагоналей ромба и его площадь.

Собственно говоря, из площади ромба:

$S_{ABCD} =\frac{1}{2} *BD*AC$

Найдём диагональ AC:

$AC = \frac{2*S_{ABCD}}{BD} =\frac{1536}{20} = \frac{384}{5}$

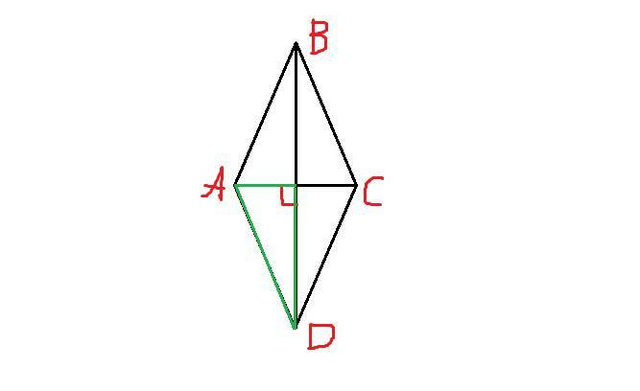
Из рисунка видно, что треугольник AOD - прямоугольный. Отсюда теорема Пифагора для нахождения гипотенузы AD:

$AD = \sqrt[2]{AO^{2} + DO^{2}}=\sqrt[2]{(\frac{192}{5})^{2} + 10^{2} }=\sqrt[2]{\frac{36864+2500}{25}}=\frac{\sqrt[2]{39364}}{5} = 39,68$

Не могу быть уверен, что ответ точный, ибо, во-первых, медиана вводит меня в заблуждение, во-вторых, ответ получился полно некрасивым, но попытка не пытка.

Площадь ромба ABCD=768, DM-медиана треугольника АВD, MD=BD =20.Найдите AD ​

Площадь ромба ABCD=768, DM-медиана треугольника АВD, MD=BD =20.Найдите AD