Ответ:
1. Треугольник прямоугольный, АВ=8 см.
2. HB=6 см.
3. AB=8 см
4. AOC=135°
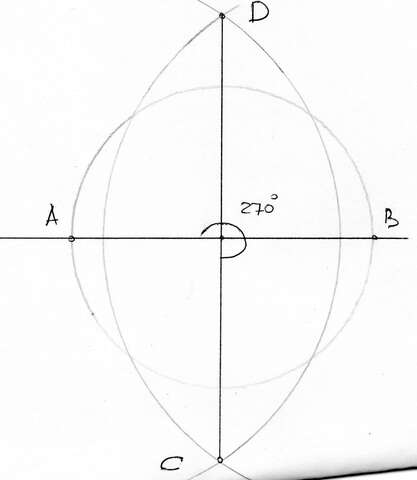
5. Смотри на картинке
Объяснение:
1. Оставшийся угол можно вычислить вычитанием имеющихся из 180°
180-30-60=90° Стало быть треугольник прямоугольный.
В прямоугольном треугольнике, катет лежащий напротив угла в 30° равен половине гипотенузы, из чего можно вычислить AB=2*AC= 8см
2. В треугольнике ABC, катет CB, лежащий на против угла 30° равен половине гипотенузы, значит
СB=AB/2=24/2=12 см.
Оставшийся угол в треугольнике ABC равен 180-90-30=60°
В треугольнике CHB, угол HCB равен 180-90-60=30°
Аналогично первому треугольнику катет лежащий напротив угла в 30° равен половине гипотенузы, а именно
HB=CB/2=12/2=6 см.
3. Вычисляем оставшийся угол треугольника 180-90-60=30°
Аналогично первым двум заданиям в треугольнике BB1A,
AB=2BB1=2*4=8 см
4. В треугольнике AOC, углы OAC=BAC/2 и OCB=BCA/2, так как биссектрисы делят углы пополам.
OAC=BAC/2=60/2=30°
OCB=BCA/2=30/2=15°
Оставшийся угол AOC=180-30-15=135°
5. Для построения угла в 270 градусов можно например воспользоваться циркулем и линейкой,
1. Рисуем произвольную прямую,
2. Выбираем произвольную точку на ней.
3. чертим окружность произвольного радиуса на пересечении с прямой получаем точки A и B
4. Из точек A и B чертим дуги с одинаковым радиусом, большим чем радиус первой окружности, на пересечении дуг получаем точки D и C
5. Соединив D и C получаем перпендикуляр к изначальной прямой.
угол, а так как 90*3=270°, три части из четырех будут нужным углом.