Ответ:
Объяснение:
1.
a) f('x)=(13-8x³+17x⁴-1)'=-24x²+68x³.
б) f'(x)=(sin(4x)+3*cos(3x))'=4*cos(4x)-9*sin(3x).
в) f'(x)=(7ˣ+6*5ˣ)'=7ˣ*ln(7)+6*5ˣ*ln(5).
г) f'(x)=((4x+5)⁵)'=5*(4x+5)⁴*(4x+5)'=5*4*(4x+5)⁴=20*(4x+5)⁴.
2.
y=3x⁴+8x²-7 x₀=1 yk=?
yk=y(x₀)+y'(x₀)*(x-x₀)
y(x₀)=3*1⁴+8*1²-7=3+8-7=4
y'=12*x³+16*x
y'(x₀)=12*1³+16*1=12+16=28 ⇒
yk=4+28*(x-1)=4+28x-28
yk=28x-24.
Ответ: yk=28x-24.
3.
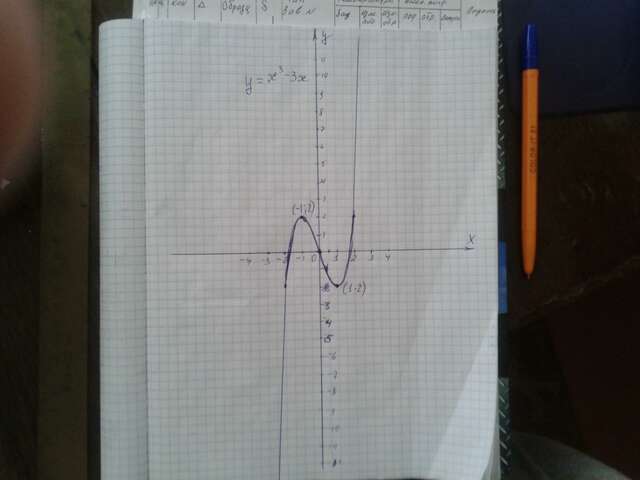
y=x³-3x
1. Точки максимума и миниума:
y'=(x³-3x)'=3x²-3=3*(x²-1)=3*(x²1)=0 |÷3
x²-1=0
(x+1)*(x-1)=0
x₁=-1 y₁=(-1)³-3*(-1)=-1+3=2 ⇒ (-1;2) = max
x=1 y₂=1³-3*1=1-3=-2 ⇒ (1;-2) = min.
2. Интервалы возрастания и убывания:
(x+1)(x-1)>0
-∞__+__-1__-__1__+__+∞ ⇒
Функция возрастает в диапазоне x∈(-∞;-1)U(1;+∞).
Функция убывает в диапазоне x∈(-1;1).
3. Точка перегиба:
y''=(y')'=(x²-1)'=2x=0 |÷2
x=0.
4. Выпуклость и вогнутость:
-∞____-____0____+____+∞
Выпуклость x∈(-∞;0)
Вогнутость x∈(0;+∞). ⇒