Апофема правильной четырехугольной пирамиды равна а, плоский угол при вершине равен...

Question

Дан 1 ответ

_zn · Answer 1 · 2020-06-01T23:13:46+0000

Ответ:

Объяснение:

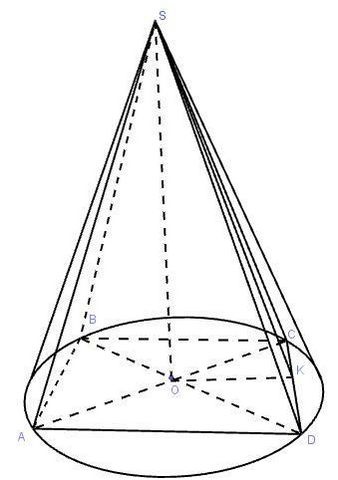
Конус можно описать около пирамиды, если ее основание - многоугольник, вписанный в окружность, а вершина пирамиды проецируется в центр этой окружности. Радиус конуса равен радиусу этой окружности, а высоты конуса и пирамиды совпадают.

∠DSC = α и SK = a — по условию.

SK - медиана, биссектриса, высота равнобедренного треугольник SCD, тогда из прямоугольного треугольника SKD:

${\rm tg}\,\frac{\alpha}{2}=\dfrac{CK}{SK}~~~\Longleftrightarrow~~~~ CK=a{\rm tg}\, \frac{\alpha}{2}$

$CD=2CK=2a{\rm tg}\, \frac{\alpha}{2}$

$BD=CD\sqrt{2}=2a\sqrt{2}{\rm tg}\, \frac{\alpha}{2}~~~\Longrightarrow ~~~~ OD=a\sqrt{2}{\rm tg}\, \frac{\alpha}{2}$

$OK=\dfrac{CD}{2}=a{\rm tg}\, \frac{\alpha}{2}$

Из прямоугольного треугольника SOK, найдем высоту SO

$SO=\sqrt{SK^2-OK^2}=\sqrt{a^2-a^2{\rm tg}^2\frac{\alpha}{2}}=a\sqrt{1-{\rm tg}^2\frac{\alpha}{2}}$

Vпирамиды: $\dfrac{1}{3}S_oh=\dfrac{1}{3}\cdot4a^2{\rm tg}^2\frac{\alpha}{2}\cdot a\sqrt{1-{\rm tg}^2\frac{\alpha}{2}}=\dfrac{4}{3}a^3{\rm tg}^2\frac{\alpha}{2}\sqrt{1-{\rm tg}^2\frac{\alpha}{2}}$ куб. ед.

Vконуса: $\dfrac{1}{3}S_oh=\dfrac{1}{3}\cdot \pi\cdot 2a^2{\rm tg}^2\frac{\alpha}{2}\cdot a\sqrt{1-{\rm tg}^2\frac{\alpha}{2}}=\dfrac{2\pi a^3}{3}{\rm tg}^2\frac{\alpha}{2}\sqrt{1-{\rm tg}^2\frac{\alpha}{2}}$ куб. ед.