Ответ:
Пошаговое объяснение:
1.
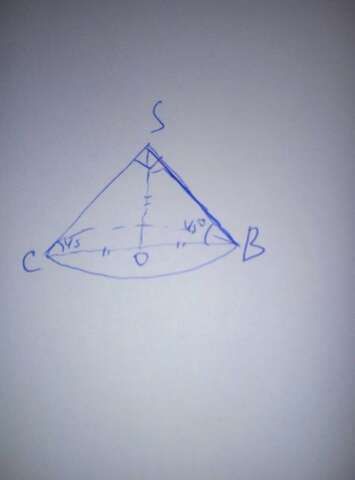
Из прямоугольного тр-ка CDB(D=90°) найдем СB=CD/sin60°
CB=6/(√3/2)=12/√3=4√3 - диаметр окружности
BSC - равнобедренный тр-к осевого сечения. SO-высота конуса, и высота тр-ка BSC.
Из прям-го треуг-ка BOS(∠O=90°) определим SO
SO/OB=tgB=tg60°
SO=OB*tg60°
OB=1/2BC=4√3/2=2√3
SO=2√3*√3=6
Vk=1/3* π*(OB)²*SO
Vk=1/3*π*12*6=24*π(cm³)
2. Scеч=1/2 ВС*SO ВSC - осевое сечение, равнобедренный тр-к (∠S=90°, ∠B=∠C=45°)
SOB - тоже равнобедренный прямоугольный(т.к ∠В=45° и ∠ВSO=45°), тогда SO=ОВ, OB=1/2 ВС
ВС- диаметр, SO - высота
Scеч=1/2 ВС*SO=OB*SO=OB²
OB²=9 OB=3(м)
Vk=1/3πOB²*SO=1/3π*OB³
Vk=π*1/3*27=9π(м³)