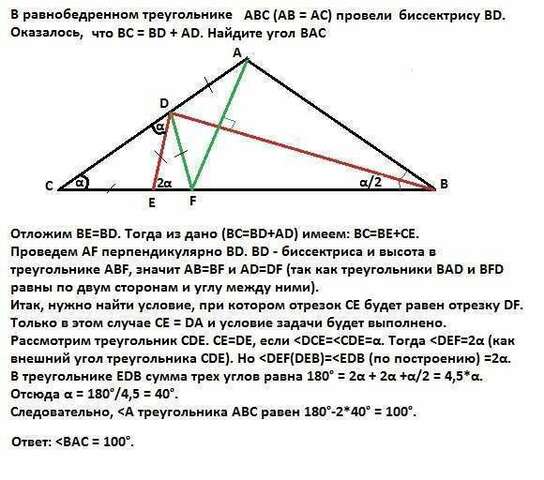
Отложим ВЕ=ВD. Тогда из дано (ВС=ВD+АD) имеем: ВС=ВЕ+СЕ.
Проведем AF перпендикулярно ВD. ВD - биссектриса и высота в треугольнике ABF, значит АВ=ВF и АD=DF (так как треугольники ВАD и ВFD равны по двум сторонам и углу между ними).
Итак, нужно найти условие, при котором отрезок СЕ будет равен отрезку DF. Только в этом случае СЕ = DA и условие задачи будет выполнено.
Рассмотрим треугольник СDЕ. СЕ=DE, только если В треугольнике ЕDВ сумма трех углов равна 180° = 2α + 2α + α/2 = 4,5*α.
Отсюда α = 180°/4,5 = 40°. Следовательно, <А треугольника АВС равен 180°-2*40°= 100°. <br>Ответ: <ВАС = 100°. <br>