Найти угол наклона касательной к кривой y=-2x^3+x, в точке, абсцисса которой равна 4

Question

Найти угол наклона касательной к кривой y=-2x^3+x, в точке, абсцисса которой равна 4

Answer 1

Угол наклона касательной к графику функции задаётся значением первой производной от функции в точке касания.  А именно f'(x0)=tga.

y'= -6x^2+1

y'(4)= -96+1= -95

a=180-arctg(95)

Где a это угол наклона.

---

Comments

А почему арктангенс?

---

Потому что tga=-95=>a=arctg(-95) это угол между прямой Ох а угол задаётя в противоположную сторону то есть угол - 180-arctg(-95)

---

Да только угол отрицательный поэтому +arctg(-95) или -arctg(95)

Answer 2

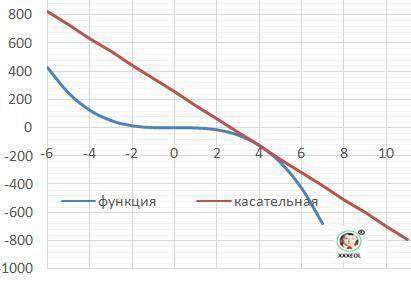
Дано: F(x)= -2*x³ + x  - функция,  Хо = 4.

Найти: Угол наклона касательной.

Решение.

Y = F'(Xo)*(x - Xo) + F(Xo) .

Находим первую производную - k - наклон касательной.

F'(x) = -6 *x² + 1.

Вычисляем в точке Хо = 4.

F'(4) = -95 - производная и

F(4) = -124 -  функция.

Записываем уравнения прямой.

Y =  -95*(x  - 4) - 124 =  -95*x  + 256 - касательная

tgα = k = - 95 - ответ.  

Надо думать что спрашивали не про САМО ЗНАЧЕНИЕ УГЛА, а именно про этот тангенс. Привлечём силу Разума и находим значение самого угла

α = arctg(-95) = 1.5813 рад ≈ 90,6° = 90°36'11" - угол наклона - ответ

Рисунок к задаче в приложении (Наклон с учетом масштабов по осям.

---