Ответ: 
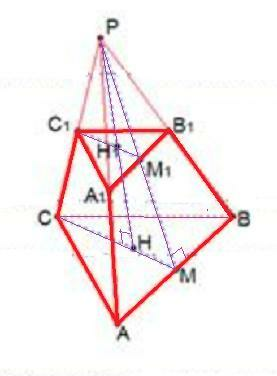
Объяснение: РАВС - правильная треугольная пирамида, АВ=12 , РН=8, А₁В₁С₁║АВС .
АСВ – правильный треугольник, Н – центр данного треугольника (центр вписанной и описанной окружностей). РМ – апофема заданной пирамиды. ММ₁ – апофема усеченной пирамиды. Согласно свойству параллельных плоскостей (две параллельные плоскости пересекают любую третью плоскость так, что линии пересечения параллельны), имеем несколько пар подобных треугольников с равным коэффициентом подобия. В частности

Найдём НМ - радиус вписанной окружности в правильный треугольник:

Рассм. ΔРНМ: