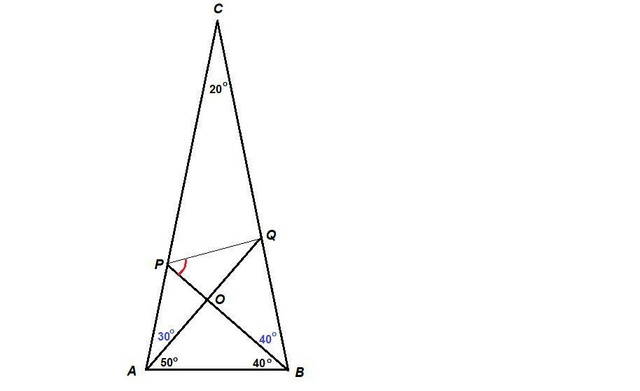
Ответ:
60°
Объяснение:
Углы при основании равнобедренного треугольника равны:
∠САВ = ∠СВА = (180° - ∠С) / 2 = (180° - 20°) / 2 = 80°
∠РАQ = ∠САВ - ∠QAB = 80° - 50° = 30°
∠QBP = ∠CBA - ∠PBA = 80° - 40° = 40°
Тогда ВР - биссектриса угла СВА.
Из ΔАОВ:
∠АОВ = 180° - (∠ОАВ + ∠ОВА) = 180° - (50° + 40°) = 90°
Тогда ВО ⊥ AQ.
Итак, ВО - высота и биссектриса ΔAQB, значит он равнобедренный, значит ВО и медиана, ⇒ АО = OQ.
В ΔAPQ РО - высота и медиана, значит он равнобедренный с основанием AQ.
Углы при основании равны:
∠PQA = ∠PAQ = 30° (или ∠PQO = 30°)
Тогда из прямоугольного треугольника POQ :
∠OPQ = 90° - ∠PQO = 90° - 30° = 60°
∠BPQ = 60°