Ответ: 16√3 м
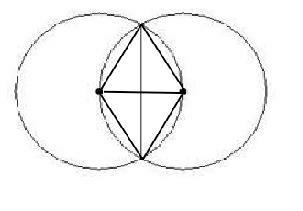
Объяснение: Соединим концы хорды с центрами окружностей и проведем отрезок между центрами окружностей. Все получившиеся отрезки равны радиусу. Поэтому получившийся четырехугольник - ромб, а данная хорда - его большая диагональ D.
Для решения задачи можно использовать разные методы. Один из них - свойство параллелограмма: сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей.
Для ромба 4а²=d²+D².
Стороны ромба и равны радиусу. т.е. 16 м.
4•16²=16²+D² ⇒
D²=4•16²-16²=3•16²
D=√(3•16²)= 16√3 (м)