Ответ:
∠NOP=70°
∠NPO=90°
∠PNO=20°.
Объяснение:
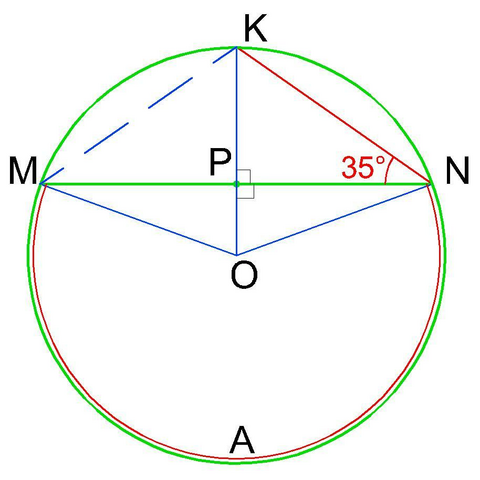
Рассмотрим ΔМКН. Он образован двумя равными прямоугольными ΔKNP и ΔKMP (т.к. PM=PN, PK-общая и ∠MPK=∠NPK=90°).
Следовательно, ΔМКН равнобедренный, с известным углом при основании ∠KNP=35°. Значит ∠MKN=180-2*35=110°.
∠MKN является вписанным углом, опирающимся на дугу А, и, по свойству вписанных и центральных углов окружности, равен половине угловой величины дуги А.
Рассмотрим ΔMON. Он равнобедренный (из равенства OM и ON) с биссектрисой (она же медиана и высота) OP.
В ΔMON ∠MON - дополняющий до 360° угловую величину дуги А.
Тогда ∠MON=360-2·∠MKN=140°.
∠NOP=∠MON÷2=70°
Т.к. ∠NPO=90°, то ∠PNO=180-90-70=20°.