Построить график функций квадратной функции y=-2x²+5x+3

Выделим полный квадрат.

$y=-2x^2+5x+3;y=-2(x^2-2*5x/4+(5/4)^2-(5/4)^2)+3\\y=-2(x-5/4)^2-(-2*25/16)+3\\y=-2(x-1.25)^2+49/8\\y=-2(x-1.25)^2+6.125$

Найдём нули этой функции.

$(x-5/4)^2=49/16\\x-5/4=б7/4\\x_1=12/4=3;x_2=2/4=0.5$

Найдём точку пересечения с осью Оу.

$y(0)=-2*0^2+5*0+3=3$

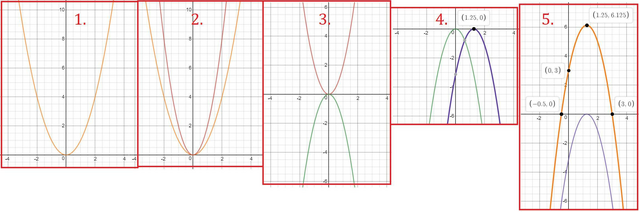
Как я буду строить: я буду последовательно изменять функции

1. Есть функция $y=x^2$ как она выглядит известно.

2. Функция $y=2x^2$ чуть уже, она сжата к оси Оу.

3. $y=-2x^2$ перевёрнута вниз (развернули на 180°).

4. $y=-2(x-1.25)^2$ график сдвинут вправо на 1.25.

5. $y=-2(x-1.25)^2+6.125$ график подняли вверх на 6.125.

Получили график нашей функции.

Точки пересечения с осями мы уже знаем, и исходя из переноса функции, можно понять какой будет координата вершины параболы.

Конечно обычно сразу отмечают координаты вершины и соединяют её с нулями функции, просто хотел объяснить по какому принципу строятся функции $y=a*f(x-b)+c$ когда известно как выглядит y=f(x).