D(f)-область определения.
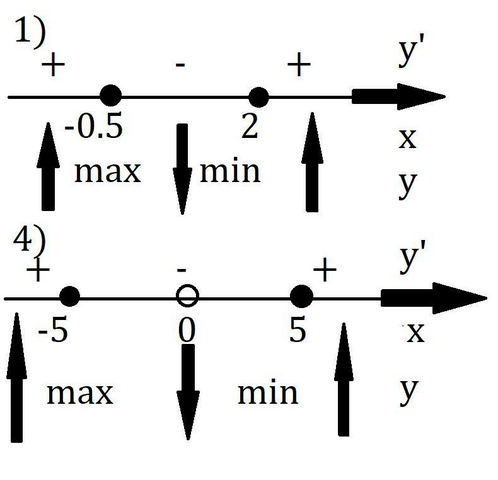
1) 
Воспользуемся методом интервалов для определения промежутков знакопостоянства выражения f'(x)
f(x) Возрастает на (-∞;-0.5)∪(2;+∞)
Убывает на (-0.5;2)
2) 
Переменная в чётной степени всегда даст не отрицательное число и выражение состоит из слагаемых, значит производная всегда положительная. И g(x) Возраста на всей области определения, то есть на (-∞;+∞)
3) 
Тут наоборот производная всегда отрицательная, то есть fi(x) убывает на (-∞;+∞)
4) 
D(ψ): (-∞;0)∪(0;+∞)

ψ(x) Возрастает на (-∞;-5)∪(5;+∞)
Убывает на (-5;0)∪(0:5)