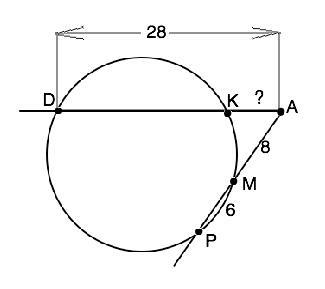
Стороны острого угла пересекают окружность так, как показано на рисунке. АМ=8, МР=6, АD=28. Найдите длину отрезка АК.
Ответ: 4
* * *
По теорема о касательной и секущей:
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на её внешнюю часть.
Следовательно, для всех секущих, проведенных из одной точки вне окружности, через одну и ту же окружность, произведения всей секущей на внешнюю часть равны. Отсюда: АD•АК=АР•АМ
28•АК=(8+6)•8 ⇒ АК=14•8:28=4 (ед. длины)